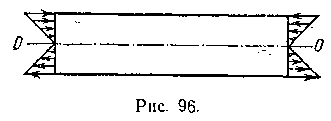Чистый изгиб
Основные положения, характеризующие деформацию чистого изгиба
Исследование напряженного состояния балок мы начнем с простейшего случая, так называемого чистого изгиба.
Чистый изгиб есть частный случай изгиба, при котором в сечениях балки поперечная сила равна нулю. Чистый изгиб может иметь место только в том случае, когда собственный вес балки настолько мал, что его влиянием можно пренебречь. Для балок на двух опорах примеры нагрузок, вызывающих чистый
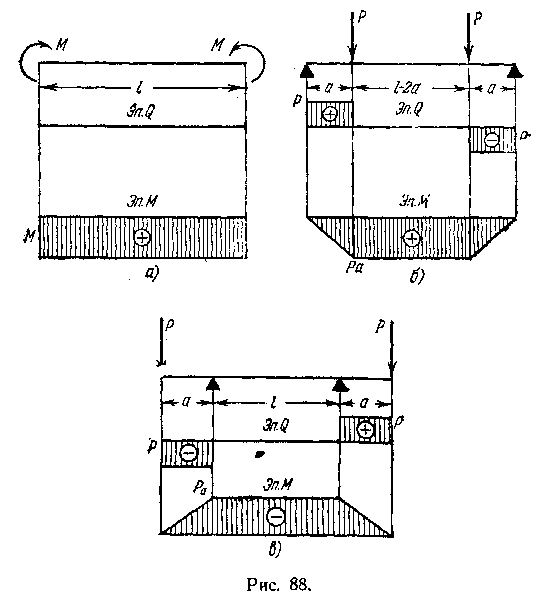
изгиб, представлены на рис. 88. На участках этих балок, где Q = 0 и, следовательно, М= const; имеет место чистый изгиб.
Усилия в любом сечении балки при чистом изгибе сводятся к паре сил, плоскость действия которой проходит через ось балки, а момент постоянен.
Напряжения могут быть определены на основании следующих соображений.
1. Касательные составляющие усилий по элементарным площадкам в поперечном сечении балки не могут быть приведены к паре сил, плоскость действия которой перпендикулярна к плоскости сечения. Отсюда следует, что изгибающее усилие в сечении является результатом действия по элементарным площадкам
лишь нормальных усилий, а потому при чистом изгибе и напряжения сводятся только к нормальным.
2. Чтобы усилия по элементарным площадкам свелись только к паре сил, среди них должны быть как положительные, так и отрицательные. Поэтому должны существовать как растянутые, так и сжатые волокна балки.
3. Ввиду того, что усилия в различных сечениях одинаковы, то и напряжения в соответственных точках сечений одинаковы.
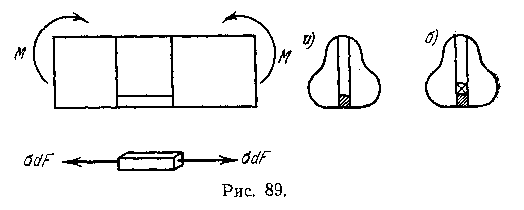
Рассмотрим какой-либо элемент вблизи поверхности (рис. 89, а). Так как по нижней его грани, совпадающей с поверхностью балки, силы не приложены, то на ней нет и напряжений. Поэтому и на верхней грани элемента нет напряжений, так как иначе элемент не находился бы и равновесии, Рассматривая соседний с ним по высоте элемент (рис. 89,б), придем к
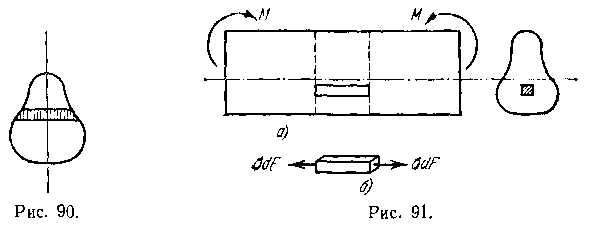
такому же заключению и т. д. Отсюда следует, что по горизонтальным граням любого элемента напряжения отсутствуют. Рассматривая элементы, входящие в состав горизонтального слоя, начиная с элемента у поверхности балки (рис. 90), придем к заключению, что и по боковым вертикальным граням любого элемента напряжения отсутствуют. Таким образом, напряженное состояние любого элемента (рис. 91,а), а в пределе и волокна, должно быть представлено так, как это показано на рис. 91,б, т. е. оно может быть либо осевым растяжением, либо осевым сжатием.
4. В силу симметрии приложения внешних сил сечение по середине длины балки после деформации должно остаться плоским и нормальным к оси балки (рис. 92, а). По этой же причине и сечения в четвертях длины балки тоже остаются плоскими и нормальными к оси балки (рис. 92,б), если только крайние сечения балки при деформации остаются плоскими и нормальными к оси балки. Аналогичное заключение справедливо и для сечений в восьмых длины балки (рис. 92, в) и т. д. Следовательно, если при изгибе крайние сечения балки остаются плоскими, то и для любого сечения остается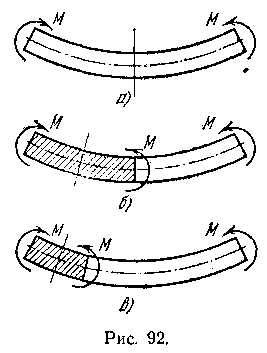
справедливым утверждение, что оно после деформации остается плоским и нормальным к оси изогнутой балки. Но в таком случае очевидно, что изменение удлинений волокон балки по ее высоте должно происходить не только непрерывно, но и монотонно. Если назвать слоем совокупность волокон, имеющих одинаковые удлинения, то из сказанного следует, что растянутые и сжатые волокна балки должны располагаться по разные стороны от слоя, в котором удлинения волокон равны нулю. Будем называть волокна, удлинения которых равны нулю, нейтральными; слой, состоящий из нейтральных волокон, — нейтральным слоем; линию пересечения нейтрального слоя с плоскостью поперечного сечения балки — нейтральной линией этого сечения. Тогда на основании предыдущих рассуждений можно утверждать, что при чистом изгибе балки в каждом ее сечении имеется нейтральная линия, которая делит это сечение на две части (зоны): зону растянутых волокон (растянутую зону) и зону сжатых волокон (сжатую зону). Соответственно с этим в точках растянутой зоны сечения должны действовать нормальные растягивающие напряжения, в точках сжатой зоны — сжимающие напряжения, а в точках нейтральной линии напряжения равны нулю.
Таким образом, при чистом изгибе балки постоянного сечения:
1) в сечениях действуют только нормальные напряжения;
2) все сечение может быть разбито на две части (зоны) — растянутую и сжатую; границей зон является нейтральная линия сечения, в точках которой нормальные напряжения равны нулю;
3) любой продольный элемент балки (в пределе любое волокно) подвергается осевому растяжению или сжатию, так что соседние волокна друг с другом не взаимодействуют;
4) если крайние сечения балки при деформации остаются плоскими и нормальными к оси, то и все ее поперечные сечения остаются плоскими и нормальными к оси изогнутой балки.
Напряженное состояние балки при чистом изгибе
Рассмотрим элемент балки, подверженной чистому изгибу, заклю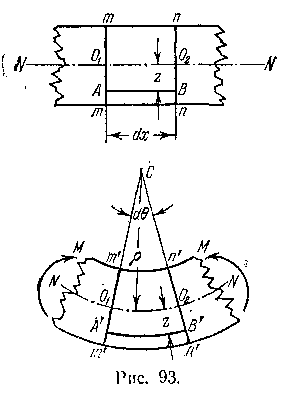 ченный между сечениями m— m и n — n, которые отстоят одно от другого на бесконечно малом расстоянии dx (рис. 93). Вследствие положения (4) предыдущего пункта, сечения m— m и n — n, бывшие до деформации параллельными, после изгиба, оставаясь плоскими, будут составлять угол dQ и пересекаться по прямой, проходящей через точку С, которая является центром кривизны нейтрального волокна NN. Тогда заключенная между ними часть АВ волокна, находящегося на расстоянии z от нейтрального волокна (положительное направление оси z принимаем в сторону выпуклости балки при изгибе), превратится после деформации в дугу А'В'.Отрезок нейтрального волокна О1О2, превратившись в дугу О1О2 не изменит своей длины, тогда как волокно АВ получит удлинение:
ченный между сечениями m— m и n — n, которые отстоят одно от другого на бесконечно малом расстоянии dx (рис. 93). Вследствие положения (4) предыдущего пункта, сечения m— m и n — n, бывшие до деформации параллельными, после изгиба, оставаясь плоскими, будут составлять угол dQ и пересекаться по прямой, проходящей через точку С, которая является центром кривизны нейтрального волокна NN. Тогда заключенная между ними часть АВ волокна, находящегося на расстоянии z от нейтрального волокна (положительное направление оси z принимаем в сторону выпуклости балки при изгибе), превратится после деформации в дугу А'В'.Отрезок нейтрального волокна О1О2, превратившись в дугу О1О2 не изменит своей длины, тогда как волокно АВ получит удлинение:
до деформации
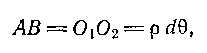
после деформации
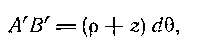
где р — радиус кривизны нейтрального волокна.
Поэтому абсолютное удлинение отрезка АВ равно
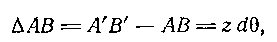
и относительное удлинение
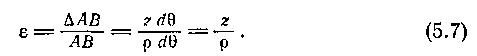
Так как согласно положению (3) волокно АВ подвергается осевому растяжению, то при упругой деформации

Отсюда видно, что нормальные напряжения по высоте балки распределяются по линейному закону (рис. 94). Так как равнодействующая всех усилий по всем элементарным площадкам сечения должна равняться нулю, то

откуда, подставляя значение из (5.8), найдем

Но последний интеграл есть статический момент относительно оси Оу, перпендикулярной к плоскости действия изгибающих усилий.
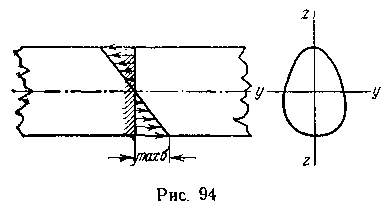
Вследствие равенства его нулю эта ось должна проходить через центр тяжести О сечения. Тамим образом,нейтральная линия сечения балки есть прямая уу, перпендикулярная к плоскости действия изгибающих усилий. Ее называют нейтральной осью сечения балки. Тогда из (5.8) следует, что напряжения в точках, лежащих на одинаковом расстоянии от нейтральной оси, одинаковы.
Случай чистого изгиба, при котором изгибающие усилия действуют только в одной плоскости, вызывая изгиб только в этой плоскости, является плоским чистым изгибом. Если названная плоскость проходит через ось Oz, то момент элементарных усилий относительно этой оси должен быть равен нулю, т. е.

Подставляя сюда значение σ из (5.8), находим

Стоящий в левой части этого равенства интеграл, как известно, является центробежным моментом инерции сеченияотносительно осей у и z, так что
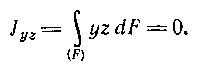
Оси, относительно которых центробежный момент инерции сечения равен нулю, называют главными осями инерции этого сечения. Если они, кроме того, проходят через центр тяжести сечения, то их можно назвать главными центральными осями инерции сечения. Таким образом, при плоском чистом изгибе направление плоскости действия изгибающих усилий и нейтральная ось сечения являются главными центральными осями инерции последнего. Иными словами, для получения плоского чистого изгиба балки нагрузка к ней не может прикладываться произвольно: она должна сводиться к силам, действующим в плоскости, которая проходит через одну из главных центральных осей инерции сечений балки; при этом другая главная центральная ось инерции будет являться нейтральной осью сечения.
Как известно, в случае сечения, симметричного относительно какой-либо оси, ось симметрии является одной из главных центральных осей инерции его. Следовательно, в этом частном случае мы заведомо получим чистый изгиб, приложив соответствующие анагрузки в плоскости, проходящей через продольную ось балки я ось симметрии ее сечения. Прямая, перпендикулярная к оси симметрии и проходящая через центр тяжести сечения, является при этом нейтральной осью этого сечения.
Установив положение нейтральной оси, нетрудно найти и величину напряжения в любой точке сечения. В самом деле, так как сумма моментов элементарных усилий относительно нейтральной оси уу должна равняться изгибающему моменту, то

откуда, подставляя значение σ из (5.8), найдем

Так как интеграл 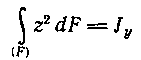 является. моментом инерции сечения относительно оси уу, то
является. моментом инерции сечения относительно оси уу, то

и из выражения (5.8) получим

Произведение ЕIУназывают жесткостью балки при изгибе.
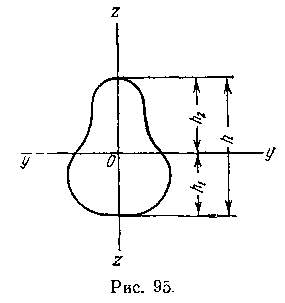
Наибольшее растягивающее и наибольшее по абсолютной величине сжимающее напряжения действуют в точках сечения, для которых абсолютная величина z наибольшая, т. е. в точках, наиболее удаленных от нейтральной оси. При обозначениях, рис. 95 имеем
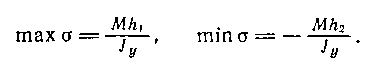
Величину Jy/h1 называют моментом сопротивления сечения растяжению и обозначают Wyр; аналогично, Jy/h2называют моментом сопротивления сечения сжатию
и обозначают Wyc,так что
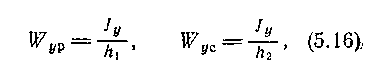
и поэтому
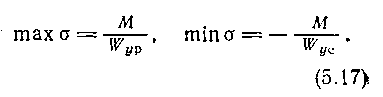
Если нейтральная ось является, осью симметрии сечения, то h1 = h2 = h/2 и, следовательно, Wyp = Wyc, так что их различать нет надобности, и пользуются одним обозначением:
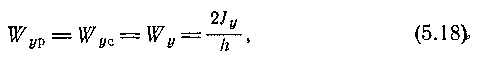
называя Wyпросто моментом сопротивления сечения.Следовательно, в случае сечения, симметричного относительно нейтральной оси,

Все приведенные выше выводы получены на основании допущения, что поперечные сечения балки, при изгибе остаются плоскими и нормальными к ее оси (гипотеза плоских сечений). Как было показано, это допущение справедливо только в том случае, когда крайние (концевые) сечения балки при изгибе остаются плоскими. С другой стороны, из гипотезы плоских сечений следует, что элементарные усилия в таких сечениях должны распределяться по линейному закону. Поэтому для справедливости полученной теории плоского чистого изгиба необходимо, чтобы изгибающие моменты на концах балки были приложены в виде элементарных сил, распределенных по высоте сечения по линейному закону (рис. 96), совпадающему с законом распределения напряжений по высоте сечения балки. Однако на основании принципа Сен-Венана можно утверждать, что изменение способа приложения изгибающих моментов на концах балки вызовет лишь местные деформации, влияние которых скажется лишь на некотором расстоянии от этих концов (приблизительно равном высоте сечения). Сечения же, находящиеся во всей остальной части длины балки, останутся плоскими. Следовательно, изложенная теория плоского чистого изгиба при любом способе приложения изгибающих моментов справедлива только в пределах средней части длины балки, находящейся от ее концов на расстояниях, приблизительно равных высоте сечения. Отсюда ясно, что эта теория заведомо неприменима, если высота сечения превосходит половину длины или пролета балки.