Определение перемещений в упругих системах

Заказать решение

Любая конструкция под действием приложенных внешних нагрузок изменяет в той или иной степени свою форму и размеры – деформируется. Для проверки жесткости и устойчивости конструкции необходимо уметь определять перемещения, вызванные деформацией ее элементов. Кроме того, определение перемещений конструкции является важнейшей вспомогательной задачей сопромата при расчете статически неопределимых систем.

Методы определения этих перемещений весьма разнообразны. Они отличаются друг от друга главным образом степенью сложности и областью применения.

Исторически первым предложенным методом определения перемещений можно считать метод непосредственного интегрирования дифференциального уравнения упругой линии балки. Однако в случае балок с большим количеством участков реализация этого метода сопряжена со значительными трудностями, которые заключаются не в интегрировании дифференциальных уравнений, а в технике определения произвольных постоянных интегрирования – составлении и решении систем линейных алгебраических уравнений.

Если по условиям нагружения балка разбивается на n участков, то задача становится очень трудоемкой уже при n=3. Для уменьшения большого объема вычислительной работы, связанной с определением произвольных постоянных интегрирования, разработан ряд методов, из которых, прежде всего, отметим метод начальных параметров, позволяющий при любом числе участков свести решение к отысканию только двух постоянных – прогиба и угла поворота в начале координат.
Указанные методы, как и некоторые другие, носят частный характер. С некоторой натяжкой их можно признать удобными при решении ограниченного круга простейших задач.
Наиболее общим методом определения перемещений в стержневых системах является метод Мора (иногда говорят: Максвелла – Мора), в основе которого лежат два основных принципа механики: начало возможных перемещений и закон сохранения энергии. Прежде чем перейти к изложению метода, остановимся на его основных теоретических предпосылках.

Обобщенные силы и обобщенные перемещения

Работа постоянной силы F на перемещений по ее направлению равна произведению величины силы на указанное перемещение: .

В задачах механики внешняя нагрузка отличается большим разнообразием и обычно представляет собой группы сил. Выражения для какой-либо группы постоянных сил можно представить в виде произведения двух величин:

, (2.1)

одна из которых – F – зависит только от сил группы и называется обобщенной силой, а другая - - зависит от перемещений и называется обобщенным перемещением.

Таким образом, под обобщенной силой будем понимать любую нагрузку (сосредоточенные силы, сосредоточенные пары, распределенную линейную нагрузку, распределенную моментную нагрузку), а под обобщенным перемещением – тот вид перемещения, на котором обобщенная сила производит работу.

Обобщенные перемещения принято обозначать буквами или с двумя индексами. Первый индекс обозначает точку и направление перемещения, а второй указывает причину, вызвавшую искомое перемещение. Например, обозначает перемещение точки приложения силы F по направлению ее действия, вызванное этой же силой.
Для обозначения полного перемещения точки, вызванного несколькими обобщенными силами, при сохраняется только первый индекс.

Перемещение, вызванное безразмерной единичной силой ;или безразмерной единичной парой , обозначается символом и называется удельным.

Работа внешних сил. Потенциальная энергия

Определим работу силы F, статически приложенной к некоторой упругой системе (рис.20, а), материал которой следует закону Гука.

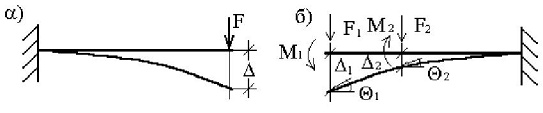
Рис. 20

При малых деформациях к этой системе применим принцип независимости действия сил, следовательно, перемещения отдельных точек и сечений конструкции прямо пропорциональны вызывающей их нагрузке:

, (2.2)

где - перемещение по направлению силы F; - некоторый коэффициент, зависящий от материала, схемы и размеров сооружения. Увеличение силы F на бесконечно малую величину dF вызовет увеличение перемещения на .

Составим выражение элементарной работы внешней силы на перемещении , отбрасывая при этом бесконечно малые величины второго порядка малости:

Заменим , используя (2.2):

Интегрируя это выражение в пределах полного изменения силы от нуля до ее конечного значения, получим формулу для определения работы, совершаемой статически приложенной внешней силой F:

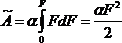
или, с учетом(2.2):

, (2.3)

то есть работа внешней силы при статическом действии ее на любое упругое сооружение равна половине произведения значения этой силы на величину соответствующего ей перемещения.

Для обобщения полученного вывода под силой понимают любое воздействие, приложенное к упругой системе, то есть не только сосредоточенную силу, но и момент или равномерно распределенную нагрузку; под перемещением понимают тот его вид, на котором данная сила производит работу: сосредоточенной силе соответствует линейное перемещение, сосредоточенному моменту – угловое, равномерно распределенной нагрузке – площадь эпюры перемещений на участке действия нагрузки.

При статическим действии на конструкцию группы внешних сил работа этих сил равна половине суммы произведений каждой силы на величину соответствующего ей перемещения, вызванного действием всей группы сил. Например, при действии на балку (рис.20,б) сосредоточенных сил F1, F2 и сосредоточенных моментов М1 и М2 работа внешних сил:

(2.4)

Работу внешних сил на вызванных ими перемещения можно выразить и иначе – через внутренние силовые факторы (изгибающие моменты, продольные и поперечные силы), возникающие в поперечных сечениях системы.

Выделим из прямолинейного стержня двумя сечениями, перпендикулярными его оси (рис.21, а), бесконечно малый элемент dz.

Стержень состоит из бесконечно большого числа таких элементов. К каждому элементу dz в общем случае плоской задачи приложены продольная сила Nz, изгибающий момент Мх и поперечная сила Qy.

Для выделенного элемента dz усилия N, M, Q являются внешними силами, поэтому работу можно получить как сумму работ, совершенных статически возрастающими усилиями N, M, Q на соответствующих деформациях элементов dz.

Рассмотрим элемент dz, находящийся только под действием продольных сил N (рис.21,б). Если его левое сечение считать неподвижным, то правое сечение под влиянием продольной силы переместится вправо на величину . На этом перемещении сила N совершит работу:

(2.5)

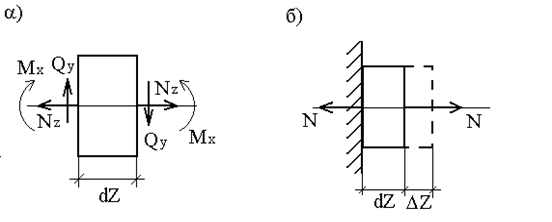
Рис. 21

Если неподвижно закрепить левое сечение элемента dz, находящегося под действием только изгибающих моментов М (рис.22,а), то взаимный угол поворота торцевых сечений элемента будет равен углу поворота его правого сечения:

На этом перемещении момент М совершит работу:

(2.6)

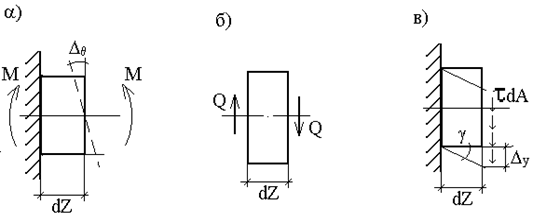
Рис. 22

Закрепим левое сечение элемента dz, находящегося под действием только поперечных сил Q (рис.22,б,в), а к правому приложим касательные усилия , равнодействующей которых является поперечная сила Q. Предположим, что касательные напряжения равномерно распределены по всей площади А поперечного сечения, то есть , тогда перемещение определяется в виде:

а работа силы Q на этом перемещении будет:

(2.7)

В действительности касательные напряжения распределены по площади поперечного сечения неравномерно, что учитывается введением в (2.7) поправочного коэффициента .

Суммируя (2.5) – (2.7), получим полное значение работы:

(2.8)

Интегрируя выражение в пределах длины L каждого участка всех стержней и суммируя результаты, получим:

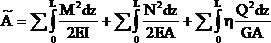(2.9)

Из формулы (2.9) следует, что работа внешних сил на вызванных ими перемещениях всегда положительна.

На основании закона сохранения энергии работа внешних сил переходит в потенциальную энергию деформации, то есть .

Теорема о взаимности работ

Рассмотрим два состояния упругой системы, находящейся в равновесии. В каждом из этих состояний на систему действует некоторая статическая нагрузка (рис.23,а). Обозначим перемещения по направлениям сил F1 и F2 через , где индекс “i” показывает направление перемещения, а индекс “j” – вызвавшую его причину.

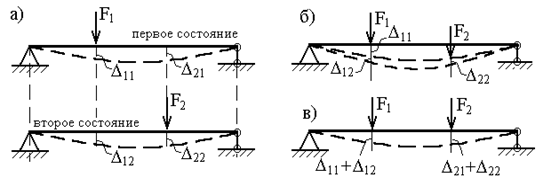
Рис. 23

Обозначим работу нагрузки первого состояния (сила F1) на перемещениях первого состояния через А11, а работу силы F2 на вызванных ею перемещениях – А22:

Используя (2.9), работы А11 и А22 можно выразить через внутренние силовые факторы:

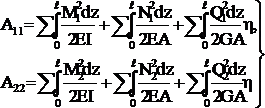(2.10)

Рассмотрим случай статического нагружения той же системы (рис.23,а) в такой последовательности. Сначала к системе прикладывается статически возрастающая сила F1 (рис.23,б); когда процесс ее статического нарастания закончен, деформация системы и действующие в ней внутренние усилия становятся такими же, как и первом состоянии (рис.23,а). Работа силы F1 составит:

Затем на систему начинает действовать статически нарастающая сила F2 (рис.23,б). В результате этого система получает дополнительные деформации и в ней возникают дополнительные внутренние усилия, такие же, как и во втором состоянии (рис.23,а). В процессе нарастания силы F2 от нуля до ее конечного значения сила F1 , оставаясь неизменной, перемещается вниз на величину дополнительного прогиба и, следовательно, совершает дополнительную работу:

Сила F2 при этом совершает работу:

Полная работа А при последовательном нагружении системы силами F1, F2 равна:

(2.11)

С другой стороны, в соответствии с (2.4) полную работу можно определить в виде:

(2.12)

Приравнивая друг к другу выражения (2.11) и (2.12), получим:

(2.13)

или

А12=А21 (2.14)

Равенство (2.14) носит название теоремы о взаимности работ, или теоремы Бетти: работа сил первого состояния на перемещениях по их направлениям, вызванных силами второго состояния, равна работе сил второго состояния на перемещениях по их направлениям, вызванных силами первого состояния.
Опуская промежуточные выкладки, выразим работу А12 через изгибающие моменты, продольные и поперечные силы, возникающие в первом и втором состояниях:

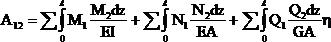(2.15)

Каждое подинтегральное выражение в правой части этого равенства можно рассматривать как произведение внутреннего усилия, возникающего в сечении стержня от сил первого состояния, на деформацию элемента dz, вызванную силами второго состояния.

Теорема о взаимности перемещений

Пусть в первом состоянии к системе приложена сила , а во втором - (рис.24). Обозначим перемещения, вызванные единичными силами (или единичными моментами ) символом . Тогда перемещение рассматриваемой системы по направлению единичной силы в первом состоянии (то есть вызванное силой ) - , а перемещение по направлению силы во втором состоянии - .

На основании теоремы о взаимности работ:

, но , поэтому , или в общем случае действия любых единичных сил:

(2.16)

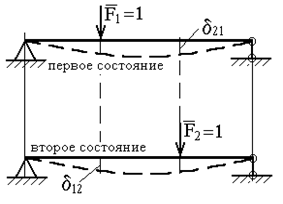
Рис. 24

Полученное равенство (2.16) носит название теоремы о взаимности перемещений (или теоремы Максвелла): для двух единичных состояний упругой системы перемещение по направлению первой единичной силы, вызванное второй единичной силой, равно перемещению по направлению второй силы, вызванному первой силой.

Вычислений перемещений методом Мора

Излагаемый ниже метод является универсальным методом определения перемещений (как линейных так и угловых), возникающих в любой стержневой системе от произвольной нагрузки.

Рассмотрим два состояния системы. Пусть в первом из них (грузовое состояние) к балке приложена любая произвольная нагрузка, а во втором (единичное состояние) – сосредоточенная сила (рис.25).

Работа А21 силы на перемещении , возникающем от сил первого состояния:

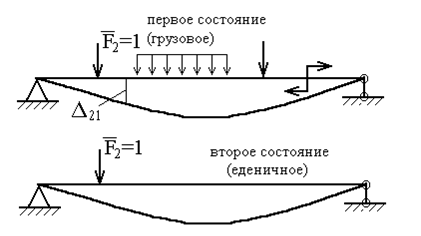
Рис.25

Используя (2.14) и (2.15), выразим А21 (а, значит, и ) через внутренние силовые факторы:

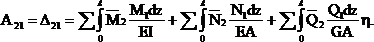(2.17)

Знак “+”, полученный при определении , означает, что направление искомого перемещения совпадает с направлением единичной силы. Если определяется линейное смещение, то обобщенная единичная сила представляет собой безразмерную сосредоточенную единичную силу, приложенную в рассматриваемой точке; а если определяется угол поворота сечения, то обобщенная единичная сила – это безразмерный сосредоточенный единичный момент.

Иногда (2.17) записывается в виде:

(2.18)

где - перемещение по направлению силы , вызванное действием группы сил . Произведения, стоящие в знаменателе формулы (2.18), называются соответственно жесткостями при изгибе, растяжении (сжатии) и сдвиге; при постоянных по длине размерах сечения и одинаковом материале эти величины можно выносить за знак интеграла. Выражения (2.17) и (2.18) называются интегралами (или формулами) Мора.

Наиболее общий вид интеграл Мора имеет в том случае, когда в поперечных сечениях стержней системы возникают все шесть внутренних силовых факторов:

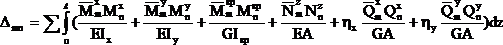(2.19)

Алгоритм вычисления перемещения методом Мора состоит в следующем:

Определяют выражения внутренних усилий от заданной нагрузки как функций координаты Z произвольного сечения.
По направлению искомого перемещения прикладывается обобщенная единичная сила (сосредоточенная сила – при вычислении линейного перемещения; сосредоточенный момент – при вычислении угла поворота).
Определяют выражения внутренних усилий от обобщенной единичной силы как функций координаты Z произвольного сечения.

4. Подставляют выражение внутренних усилий, найденные в п.п.1,3 в (2.18) или (2.19) и интегрированием по участкам в пределах всей длины конструкции определяют искомое перемещение.

Формулы Мора пригодны и для элементов, представляющих собой стержни малой кривизны, с заменой элемента длины dz в подынтегральном выражении элементом дуги ds.

В большинстве случаев плоской задачи используется только один член формулы (2.18). Так, если рассматриваются конструкции, работающие преимущественно на изгиб (балки, рамы, а частично и арки), то в формуле перемещений с соблюдением достаточной точности можно оставить только интеграл, зависящий от изгибающих моментов; при расчете конструкций, элементы которых работают, в основном, на центральное растяжение (сжатие), например, ферм, можно не учитывать деформации изгиба и сдвига, то есть в формуле перемещений останется только член, содержащий продольные силы.
Аналогично, в большинстве случаев пространственной задачи существенно упрощается формула Мора (2.19). Так, когда элементы системы работают преимущественно на изгиб и кручение (например, при расчете плоско-пространственных систем, ломаных стержней и пространственных рам) в (2.19) остаются только первые три члена; а при расчете пространственных ферм – только четвертый член.

Примеры расчетов

Пример 13.

Определить прогиб в середине пролета и угол поворота левого опорного сечения балки, нагруженной равномерно распределенной нагрузкой (рис.26,а), методом Мора.

Рассмотрим три состояния балки: первое (грузовое) – при действии заданной распределенной нагрузки q; ему соответствует эпюра моментов (рис.26,б). Второе состояние (единичное) – при действии сосредоточенной силы , приложенной в точке С; ему соответствует эпюра моментов (рис.26,в). Третье состояние (также единичное) – при действии сосредоточенного момента , приложенного в точке В; ему соответствует эпюра моментов (рис.26,г). Примем начало координат на левой опоре; тогда ординаты указанных эпюр в сечении с координатой z соответственно равны:

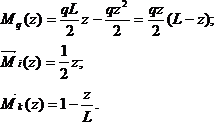
Вычисляем прогиб балки в точке С:

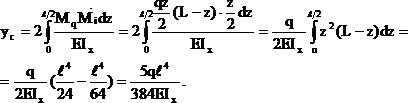
Знак "+" означает, что точка С переместится в направлении действия силы.

Вычисляем угол поворота сечения В:

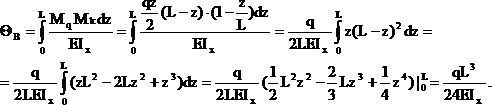
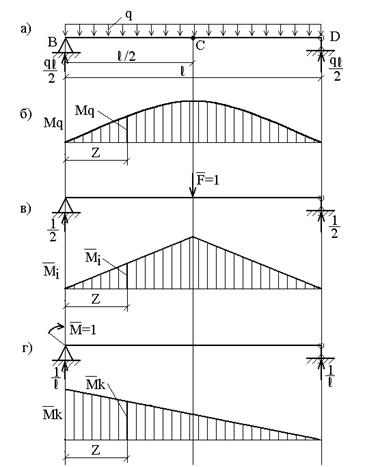
Рис. 26

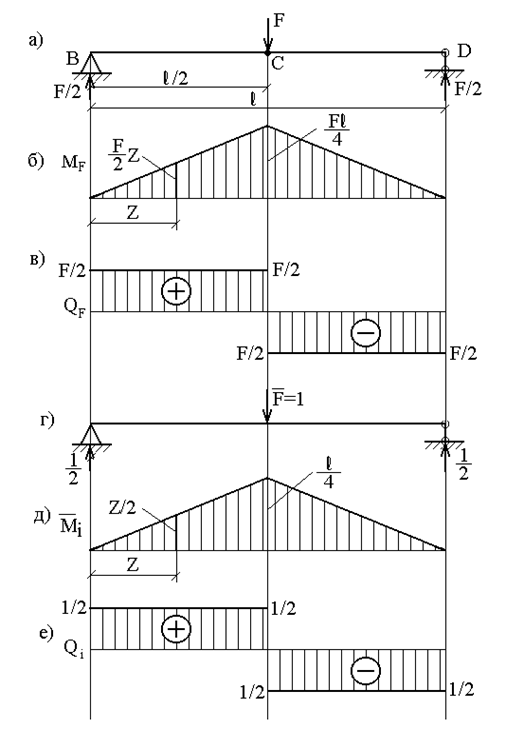
Рис. 27

Знак "+" означает, что сечение В поворачивается в направлении действия момента то есть по часовой стрелке.

Пример 14. Определить прогиб балки в середине пролета (рис.27,а) методом Мора. Оценить влияние поперечной силы на общую величину прогиба.

Рассмотрим два состояния балки. Первое состояние (грузовое) – при действии силы F (рис.27,а); ему соответствует эпюры изгибающих моментов (рис.27,б) и поперечных сил (рис.27,в).

Второе состояние (единичное) – при действии силы (рис.27,г); ему соответствуют эпюры изгибающих моментов (рис.27,д) и поперечных сил (рис.27,е).

В связи с отсутствием продольных сил в поперечных сечениях балки интеграл Мора (2.18) принимает вид:

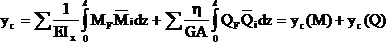
Подставляя значения изгибающих моментов и поперечных сил в сечении с координатой z (рис.27) для составляющих полного перемещения получим:

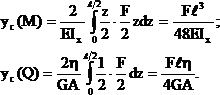
Оценим влияние поперечной силы на общую величину прогиба. Пусть рассматриваемая балка имеет прямоугольное поперечное сечение со сторонами b и h, при этом h=0,1ℓ.

Тогда площадь сечения и его осевой момент инерции равны:

Будем считать, что тогда:

то есть прогиб, обусловленный деформацией сдвига, составляет 3% от прогиба, обусловленного изгибом. Легко убедиться, что при увеличении отношения влияние поперечных сил на величину прогиба становится еще менее значительным.