Построение эпюр в ломаных стержнях

 

  Систему, состоящую из жестко соединенных между собой стержней, оси которых не лежат в одной плоскости в сопромате называют ломаным стержнем. При этом ограничимся рассмотрением только таких ломаных стержней, отдельные элементы которых стыкуются друг с другом под прямыми углами, а внешние нагрузки приложены перпендикулярно к осям стержней (рис.17,а,б).

 

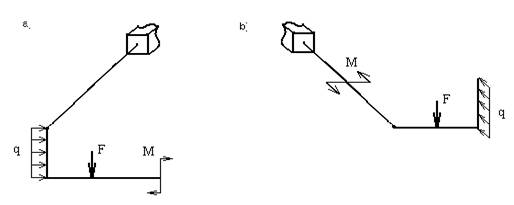
Рис.17

В общем случае нагружения в поперечных сечениях ломаных стержней могут возникать все 6 известных внутренних силовых факторов: продольная сила , поперечные силы , изгибающие моменты , крутящий момент. Очень часто, особенно в машиностроительных конструкциях, отдельные элементы ломаного стержня имеют незначительную длину, иногда соизмеримую с размерами поперечного сечения, то есть являются "короткими" стержнями. В этом случае не только внутренние моменты,, но и внутренние силы (,) существенно влияют на напряженно-деформированное состояние конструкции, поэтому для ломаных стержней будем строить эпюры всех шести внутренних силовых факторов.

Для правильного построения эпюр здесь обязательным является использование скользящей системы координат, о которой уже говорилось при рассмотрении плоско-пространственных систем (см.1.17).

  Пример 12. Рассмотрим простейший случай нагружения ломанного стержня - двумя взаимноперпендикулярными сосредоточенными силами, приложенными на свободном конце (рис.18,а).

Выбираем скользящую систему координат (рис.18,б). Ось z всегда направлена вдоль продольной оси того или иного участка ломаного стержня, а при переходе с одного участка на другой координатные оси поворачиваются на 90 градусов, но никогда не вращаются вокруг оси z. Удобнее всего начинать выбор скользящей системы координат с горизонтального участка ломаного стержня, который параллелен плоскости чертежа или лежит в этой плоскости (участок ВС на рис.18,б).
На этом участке (а он аналогичен обычной балке) ось y  направляется вертикально (вверх или вниз), ось z - вдоль продольной оси участка, а ось  x - перпендикулярно плоскости yoz, после чего система координат передвигается на остальные участки ломаного стержня.

 Построение эпюры .

Построение этой и всех последующих эпюр ведем от свободного конца. Правило знаков для  остается таким же, как и для других систем, а именно: растяжению соответствует знак "+", сжатию - "-".

Участок АВ имеет нулевую продольную силу, так как  перпендикулярны продольной оси этого участка:

.
Участок ВС растягивается силой :

.
Участок СД сжимается силой :

.

Построение эпюр  и .

Поперечную силу  формируют только те силы, которые параллельны оси x на данном участке, а поперечную силу - силы, параллельные оси y. Здесь также сохраняется обычное для Q правило знаков: , если внешняя сила, приложенная к отсеченной части, стремится повернуть рассматриваемое сечение по часовой стрелке и - в противоположном случае. С учетом сказанного в характерных сечениях имеем:

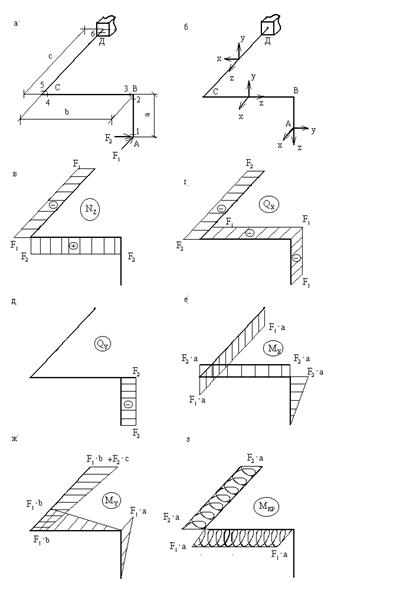
Рис.18

 

Построение эпюр .

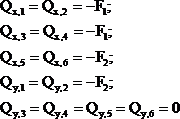
Ординаты эпюр изгибающих моментов будем, как обычно, откладывать со стороны сжатых волокон, не указывая знаков, причем ориентировать эпюры нужно так, чтобы плоскость эпюры совпадала с плоскостью действия пары того изгибающего момента, для которого она построена. Иначе говоря, эпюра  на всех участках ломаного стержня располагается в плоскости yoz, а эпюра - в плоскости xoz.

Начнем с построения эпюры . Здесь нас будет интересовать изгиб каждого участка в плоскости yoz (см. скользящую систему координат на
рис.18,б) и, соответственно, плечо каждой действующей на отсеченную часть нагрузки нужно измерять в этой плоскости.

На участке АВ плоскость yoz - вертикальная плоскость, параллельная плоскости чертежа. В этой плоскости стержень АВ изгибается только силой , так как  перпендикулярна плоскости yoz :

;
 (сжаты правые волокна).

На участке ВС плоскость yoz  ориентирована так же, как и на участке АВ, причем, все точки ВС равноудалены от линии действия силы , поэтому:
 (сжаты верхние волокна).

На участке СД плоскость yoz - вертикальная плоскость, перпендикулярная плоскости чертежа. В этой плоскости стержень СД изгибается только силой , так как  перпендикулярна yoz ; все точки участка СД равноудалены (в рассматриваемой плоскости) от линии действия силы , следовательно:

 (сжаты нижние волокна).

Рассуждая аналогичным образом, будем строить эпюру , но теперь нужно рассматривать изгиб каждого участка ломаного стержня в плоскости xoz.

На участке АВ плоскость xoz - вертикальная плоскость, перпендикулярная плоскоси чертежа. В этой плоскости стержень АВ изгибается только силой , так как  перпендикулярна плоскости xoz:

;
 (сжаты дальние от наблюдателя волокна).

На участке ВС плоскость xoz - горизонтальная плоскость. В этой плоскости сила  приложена вдоль продольной оси стержня ВС и к изгибу привести не может, поэтому:

;
 (сжаты дальние от наблюдателя волокна).

На участке СД плоскость xoz - это так же горизонтальная плоскость. Здесь к изгибу стержня СД приводят обе силы: плечо силы   постоянно и равно b, а плечо силы  равно нулю в сечении 5 и равно с в сечении 6:

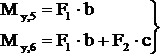  (сжаты правые волокна).

Иногда при построении эпюр изгибающих моментов в ломанных стержнях возникают затруднения в определении участия той или иной нагрузки в изгибе стержня или в определении плеча той или иной нагрузки. В этих случаях всегда можно использовать простой, но эффективный прием: спроектировать конструкцию и действующие нагрузки на ту плоскость в которой изгибается стержень, переходя тем самым от пространственной конструкции к ее проекции, что позволяет легко определить плечи каждой из нагрузок и их "вклад" в изгиб рассматриваемого участка. Проследим использование этого приема например, при построении эпюры  на участке СД (рис.18,а,б). На этом участке плоскость xoz, в которой нужно рассматривать изгиб стержня при построении - горизонтальная плоскость, следовательно, для реализации описываемого приема необходимо спроектировать конструкцию на горизонтальную плоскость, то есть изобразить вид сверху (рис.19).

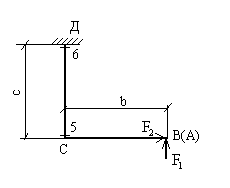
Рис.19

При этом сила  будет видна направленной вдоль стержня ВС, сила - перпендикулярно ВС, а стержень ВА проектируется в точку. Теперь совершенно очевидно, что все точки стержня СД равноудалены от линии действия силы , что приводит к постоянному моменту , а сила  имеет нулевое плечо в сечении 5 и плечо, равное с, - в сечении 6:

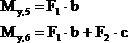
В обоих сечениях сжаты  правые волокна, то есть получен тот же результат, что и ранее, но в более наглядном виде.