Построение эпюр для плоских рам
При решении задач сопромата, плоской рамой называется стержневая система, элементы которой жестко или шарнирно соединены между собой, нагруженная в своей плоскости.
Вертикально (или под наклоном) расположенные стержни рамы называются стойками, а горизонтальные - ригелями. Жесткость узлов устраняет возможность взаимного поворота скрепленных стержней, то есть в узловой точке углы между их осями остаются неизменными.
Как и многие другие системы, рамы делятся на статически определимые и статически неопределимые (рис.10, б,в,д,е).
Промежуточный шарнир снижает степень статической неопределимости рамы на величину m - 1, где m - число стержней, сходящихся в шарнире. Если m >2, то шарнир называется кратным (рис.10,д).
Для определения степени статической неопределимости плоской рамы можно воспользоваться формулой:
n = 3К-Ш,
где n - степень статической неопределимости; К - число замкнутых контуров в предположении полного отсутствия шарниров; Ш- число шарниров в пересчете на одиночные.
Для рамы (рис.10,б) имеем:
К=1; Ш=0;
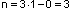
Для рамы (рис.10,д):
К=3; Ш=3
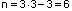
В более простых случаях, когда отсутствуют замкнутые контуры и промежуточные шарниры, то есть когда используются комбинации тех же опор, что и в балках (жесткая заделка, шарнирно-подвижная и шарнирно-неподвижная опоры), для определения степени статической неопределимости используется “балочная” формула:
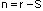
где r - число неизвестных реакций; S - число уравнений статики ( для плоской рамы S=3).
Ограничимся рассмотрением простейших статически определимых рам трех видов:
- с жесткой заделкой;
- на двух шарнирных опорах (неподвижной и подвижной);
- на двух шарнирно неподвижных опорах с простым промежуточным шарниром.
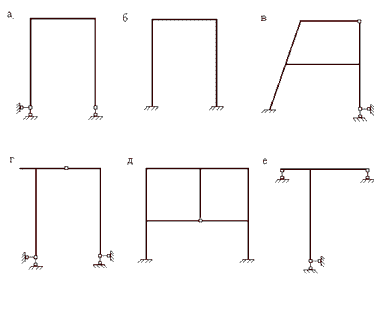
Рис. 10
Из шести внутренних силовых факторов в сечениях плоской рамы в общем случае возникают три: продольная сила Nz; поперечная сила Qy; изгибающий момент Mx.
Правила знаков. Для Nz и Qy сохраняются ранее принятые правила знаков.
Nz > 0, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, вызывает в данном сечении растяжение и Nz < 0 - в противном случае.
Qy > 0, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, стремится повернуть данное сечение по часовой стрелке и Qy < 0 - в противном случае.
Ординаты эпюр Nz и Qy (как, впрочем и Mx) откладывают, как и обычно, перпендикулярно к оси элементов рамы. Иногда положительные ординаты Nz и Qy откладывают с внешней стороны рамы, а отрицательные – с внутренней, но рама часто имеет такую конфигурацию, при которой невозможно выделить внутреннюю и внешнюю стороны, поэтому в дальнейшем условимся: ординаты эпюр Nz и Qy откладываются в произвольную сторону, но обязательно указывается знак.
Для изгибающих моментов специального правила знаков нет, а при вычислении момента в любом сечении знак принимается произвольно. Но результат вычислений всегда откладывается со стороны сжатого волокна элемента рамы. При этом знак на эпюре Mx никогда не указывается. Такое условие полностью соответствует характеру <strong>построения strong=""> Mx в балках, где в соответствии с принятым для изгибающих моментов правилом знаков (см. 1.7) ординаты эпюр Mx всегда оказывались расположенными со стороны сжатых волокон балки.
Рамы с жесткой заделкой
Пример 7.
Рассмотрим жесткозащемленную плоскую раму (рис.11,а). В жесткой заделке рамы в общем случае нагружения возникают три опорные реакции: две силы (Ha и Ra ) и опорный момент (Ma). Для построения эпюр определение этих реакций не является безусловной необходимостью: расчет, как и в случае жесткозащемленной балки, можно вести от свободного конца, то есть всякий раз так выбирать отсеченную часть для рассматриваемого сечения, чтобы в нее не попадала опора с неизвестными опорными реакциями. Тем не менее, иногда целесообразно вычислить опорные реакции. Это позволяет проверить построение эпюр или облегчить их построение. Для вычисления реакций в жесткозащемленной раме используются три условия равновесия:
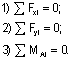
Построим эпюры Nz, Qy, Mx для рассматриваемой рамы, не вычисляя опорные реакции.
Методика построения эпюр аналогична ранее рассмотренной для балок , т.е. сначала необходимо наметить характерные сечения. В дополнение к ранее указанным (см.1.2), в рамах характерными являются также сечения, расположенные бесконечно близко к жесткому узлу на всех элементах, сходящихся в этом узле.
Построение эпюры Nz. Следуя установленным правилам, в рассматриваемой раме можно выделить 8 характерных сечений. Продольная сила в любом из них численно равна алгебраической сумме проекций всех сил, приложенных по одну сторону от рассматриваемого сечения, на продольную ось стержня. При этом следует учитывать, что положение продольной оси будет изменяться в зависимости от того, чему принадлежит рассматриваемое сечение - стойкам или ригелю.
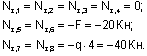
Построение эпюры Qy. Поперечная сила в любом сечении численно равна алгебраической сумме проекций всех сил, приложенных по одну сторону от рассматриваемого сечения, на поперечную ось рамы. Положение поперечной оси также будет изменяться в зависимости от принадлежности данного сечения стойкам или ригелю. С учетом правила знаков, двигаясь от свободного конца к жесткой заделке, получим для Qy:
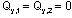 (проекция пары М на любую ось равна нулю);
(проекция пары М на любую ось равна нулю);
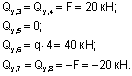
Необходимо обратить внимание на тот факт, что 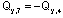 , т.е. что поперечная сила в верхних сечениях противоположных стоек от действия силы, приложенной к правой стойке (при заделке, расположенной слева, и наоборот) имеет противоположные знаки. Отчасти это можно объяснить противоположными направлениями оси y для сечений 4 и 7, но более строгое обоснование указанного равенства будет дано ниже.
, т.е. что поперечная сила в верхних сечениях противоположных стоек от действия силы, приложенной к правой стойке (при заделке, расположенной слева, и наоборот) имеет противоположные знаки. Отчасти это можно объяснить противоположными направлениями оси y для сечений 4 и 7, но более строгое обоснование указанного равенства будет дано ниже.
Построение эпюры Mx. Изгибающий момент в любом сечении численно равен алгебраической сумме моментов всех нагрузок, приложенных по одну сторону от рассматриваемого сечения, относительно этого сечения (более строго: относительно оси x этого сечения). Обратим внимание на два важных замечания:
- составляющая момента Mx от действия сосредоточенного момента М всегда одинакова и равна М;
- под плечом силы всегда понимается длина перпендикуляра, опущенного из центра тяжести данного сечения на линию действия силы. Это означает, что, например, плечо силы F для сечений 4-7 одинаково и равно 3 м.
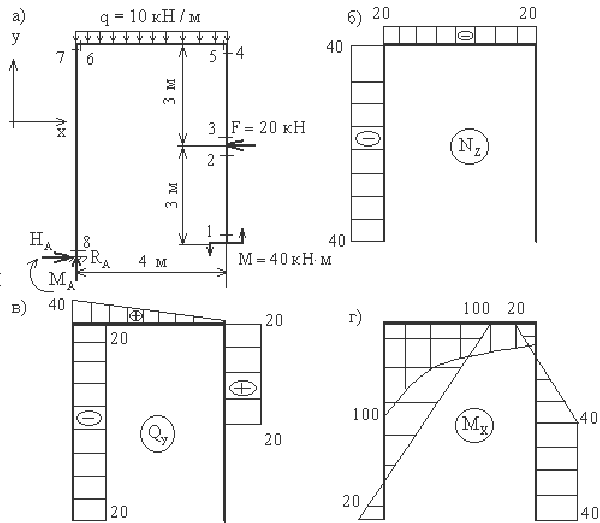
Рис. 11
Таким образом, для сечений 1-8 получим: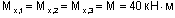
(сжатым является правое волокно в сечениях 1-3, поэтому ордината отложена вправо от оси стойки);
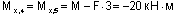
(знаки "+" и "-" здесь имеют относительный характер; результирующий момент сжимает левые волокна в сечении 4 и нижние волокна в сечении 5, поэтому ордината "20" откладывается соответственно влево и вниз);
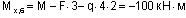
(сжаты нижние волокна);</p>
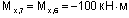
(сжаты правые волокна);
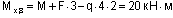
(сжаты левые волокна).
Между q, Qy и Mx в плоских рамах сохраняются те же зависимости, что и в балках, а именно: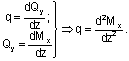
Из этого следует, что правила контроля эпюр Qy и Mx остаются теми же, что и для балок ,( см. 1.11).
Эпюры Nz в плоских рамах строятся наиболее просто и при отсутствии нагрузок, распределенных вдоль стержней, представляют собой графически отрезки прямых, параллельные осям стержней ( или совпадают с ними при Nz = 0).
Если проанализировать процесс построения эпюр (рис.11,б-г), то очевидно, что наиболее "сложно" вычислять ординаты в сечениях стержня, примыкающего к заделке ( на рис.11,б-г это сечения 7 и 8). Как уже отмечалось, с этой целью иногда вычисляют реакции Ha, Ra и момент Ma.
При принятом для всей рамы направлении осей x,y (рис.11,а) уравнения равновесия имеют вид:
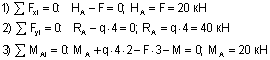
Полученный для каждой из величин Ha, Ra, Ma знак "+" говорит, что направления их были выбраны правильно.
После вычисления опорных реакций значения величин Nz, Qy, Mx в сечениях 7 и 8 (как, впрочем, и в любом другом) можно вычислять, двигаясь от жесткой заделки к свободному концу.
Например, для сечений 7 и 8:
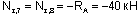
(знак "-" указывает на сжатие в этих сечениях с силой Ra);
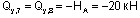
(т.к. реакция Ha стремится повернуть каждое из этих сечений против часовой стрелки.)
При сравнении величины Qy7 с ранее полученной величиной Qy4 видно, что
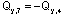 ,
,
о чем уже говорилось выше.
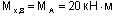
(сжаты левые волокна стойки);
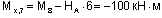
(сжаты правые волокна стойки).
Разумеется, результаты получаемые для любого сечения при движении от свободного конца к жесткой заделке и при движении в обратном направлении одинаковы.
Рамы на двух шарнирных опорах
В дальнейшем для краткости будем говорить "шарнирная рама", имея в виду ее статическую определимость и отсутствие промежуточных шарниров ( см. 1.13).
Пример 8.
Рассмотрим раму той же конфигурации, размеров и с теми же нагрузками, что и в предыдущем примере, но с шарнирным опиранием (рис.12,а).
Здесь также имеем 8 характерных сечений, но для построения эпюр необходимо вычислить сначала опорные реакции, т.к. ни для одного из сечений нельзя выбрать отсеченную часть так, чтобы избежать попадания в нее опоры с неизвестной реакцией.
Для определения опорных реакций в плоских шарнирных рамах используются следующие уравнения равновесия:
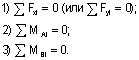
Первое уравнение равновесия используется в том из двух приведенных вариантов, который будет содержать одну неизвестную опорную реакцию.
Так, в рассматриваемом примере этим условием будет 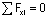 которое будет содержать неизвестную реакцию Ha (в то время как условие
которое будет содержать неизвестную реакцию Ha (в то время как условие 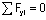 содержало бы две неизвестных реакции). Если бы опоры располагались так, что вертикальным является один стержень, то в качестве первого шага использовалось условие
содержало бы две неизвестных реакции). Если бы опоры располагались так, что вертикальным является один стержень, то в качестве первого шага использовалось условие 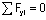 .
.
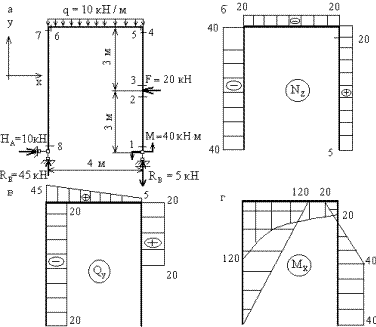
Рис. 12
Второе и третье уравнения равновесия (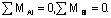 ) - такие же, как и для балок, но в одно из них обязательно войдет реакция, вычисленная из первого уравнения ( иногда - с нулевым плечом).
) - такие же, как и для балок, но в одно из них обязательно войдет реакция, вычисленная из первого уравнения ( иногда - с нулевым плечом).
В качестве проверки вычисленных реакций используется условие, противоположное первому, то есть 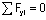 (или
(или 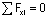 ).
).
Построение эпюр Nz, Qy, Mx в шарнирных рамах выполняется так же, как и в защемленных, но " с меньшими затратами", так как после вычисления реакций опор направление обхода рамы не играет роли, и выбор отсеченной части в каждом случае определяется ее простотой.
Вычислим реакции опор рамы (рис.12,а)
Уравнения статики:
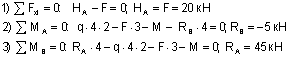
Знак "-", полученный при вычислении реакции Rb, говорит, что принятое для нее направление нужно изменить на противоположное. Выполним проверку:
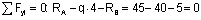 ,
,
то есть реакции опор вычислены правильно.
Построение эпюры Nz.
Двигаясь по оси рамы от сечения 1 к сечению 6, получим:
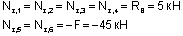
Для сечений 7 и 8 проще рассматривать отсеченную часть, продвигаясь от опоры А к сечению 7:
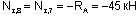
Этот же результат получим из рассмотрения отсеченной части 1-6:
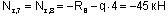
По вычисленным значениям строим эпюру Nz ( рис.12,б)
Построение эпюры Qy.
Из рассмотрения отсеченной части 1-5:
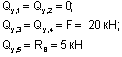
Из рассмотрения отсеченной части 8-6:
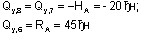
Эпюра Qy, построенная по вычисленным значениям, показана на рис.12,в.
Построение эпюры Mx.
Из рассмотрения отсеченной части 1-5:
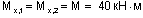 (сжаты правые волокна стойки);
(сжаты правые волокна стойки);
<img alt='" src=' images="" dlya_statey="" rama_epur="" 37.gif"="" _cke_saved_src="images/dlya_statey/rama_epur/37.gif" src="/images/"> (плечо силы F равно нулю);
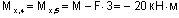 (сжаты левые волокна стойки в сечении 4 и нижние волокна ригеля в сечении 5);
(сжаты левые волокна стойки в сечении 4 и нижние волокна ригеля в сечении 5);
Из рассмотрения отсеченной части 8 -6:
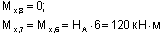
(сжаты правые волокна стойки и нижние волокна ригеля в сечениях 7 и 6 соответственно).
Эпюра Mx показана на рис12,г.
Пример 9. Рассмотрим шарнирную раму более сложной конфигурации (рис.13,а).
Здесь необходимо рассматривать 10 характерных сечений для построения эпюр Nz, Qy, Mx. Сечения 1-6 расположены на ригеле слева направо, а сечения 7-10 - на стойке сверху вниз. Как и в предыдущем примере, указанное расположение характерных сечений является безусловно необходимым, а их нумерация - произвольной.
Уравнения статики для вычисления опорных реакций имеют вид:
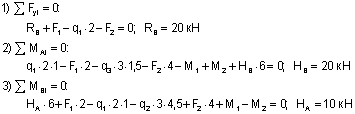
Проверка вычисления опорных реакций:
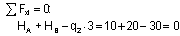
При построении эпюр Nz, Qy, Mx целесообразно выбирать отсеченную часть, продвигаясь к центральному узлу рамы с четырех сторон, т.к. в этом случае определение внутренних силовых факторов в каждом из характерных сечений осуществляется наиболее просто.
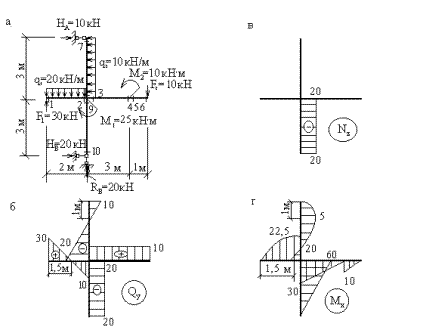
Рис. 13
Построение эпюр Nz, Qy, Mx.
Из рассмотрения левой относительно центрального узла отсеченной части (сечения 1-2):
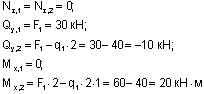
(сжаты верхние волокна).
Из рассмотрения правой отсеченной части (сечения 3-6):
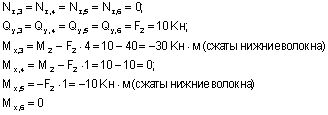
Из рассмотрения верхней относительно центрального узла отсеченной части (сечения 7-8):
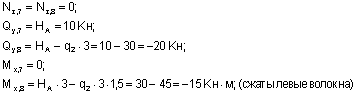
Из рассмотрения нижней отсеченной части (сечения 9-10):
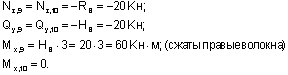
Характер эпюры Qy на участках рамы с распределенными нагрузками q1 и q2, а именно, наличие пересечений эпюры с осью рамы, говорит о том, что в этих точках момент Mx принимает экстремальные значения. Определение положений точек пересечения (т.е. тех точек, где Qy = 0) выполняется так же, как и в балках (см. 1.9).
Вычислим экстремальные значения момента Mx.
На участках под распределенной нагрузкой 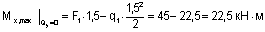
(сжаты верхние волокна).
На участке с распределенной нагрузкой 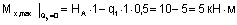
(сжаты правые волокна).
Эпюры Nz, Qy, Mx показаны на рис.13,б,в,г.
Рамы на двух опорах с промежуточным шарниром
Как отмечалось выше, рамы на двух шарнирно-неподвижных опорах с одним промежуточным шарниром также являются статически определимыми.
Пример 10. Рассмотрим построение эпюр Nz, Qy, Mx для рамы с промежуточным шарниром (рис.14,а).
В дополнение к условиям равновесия, рассмотренным в примерах 8 и 9, здесь для определения неизвестных реакций (Ha, Ra, Hb, Rb) используются еще два условия: 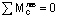 и
и 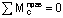 , каждое из которых по своей сути выражает факт равенства нулю изгибающего момента Mx в промежуточном шарнире С (рис.14,а).
, каждое из которых по своей сути выражает факт равенства нулю изгибающего момента Mx в промежуточном шарнире С (рис.14,а).
Для определения четырех неизвестных реакций возможно использование различных комбинаций уравнений равновесия, но чаще всего используются следующие уравнения:
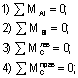
При этом для проверки вычисленных реакций служат уравнения:
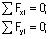
При заданных нагрузках (рис.14,а) уравнения равновесия принимают вид:
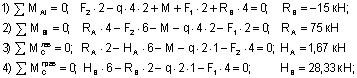
Знак "-", полученный при вычислении реакции Rb, говорит о необходимости изменить принятое для нее направление на противоположное (перечеркнутая стрелка на рис.15,а).
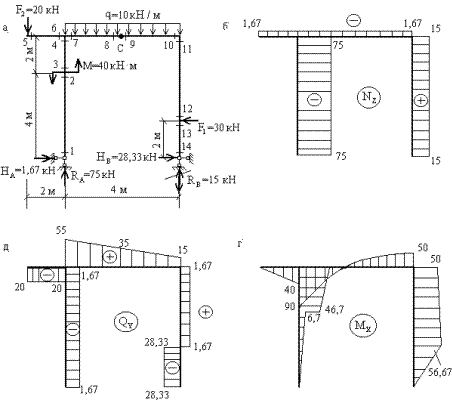
Рис 14.
Проверяем правильность вычисления опорных реакций.
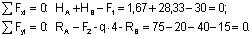
Теперь вычисляем значения Nz, Qy, Mx в характерных сечениях, выбирая для сечений 1-8 левую отсеченную часть, а для сечений 9-14 - правую.
Из рассмотрения левой отсеченной части:
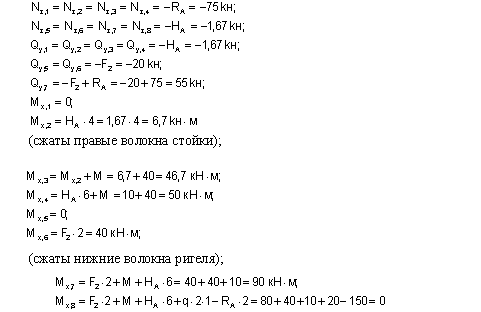
Вновь подчеркнем, что знаки "+" и "-" для изгибающих моментов Mx принимаются относительно, то есть для разграничения противоположно направленных моментов, а эпюра Mx строится со стороны сжатых волокон.
Из рассмотрения правой отсеченной части:
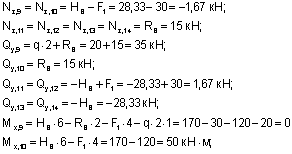
(сжаты верхние волокна ригеля)

Эпюры Nz, Qy, Mx, построенные по вычисленным значениям, приведены на рис.14,б,в,г.